La glorieuse incertitude du sport résiste-t-elle à l’analyse scientifique ? Alan Gabel et Sydney Redner, deux chercheurs de l’université de Boston (États-Unis), ont passé au crible les résultats de quatre saisons de la NBA (National Basketball Association). Leurs conclusions : les paniers marqués par les sportifs américains suivent des lois statistiques bien connus des mathématiciens.
Leur étude s’est concentrée sur la période 2006-2010, offrant tout de même un échantillon total de 6 087 matchs permettant de consolider des statistiques robustes, rendues possibles par des internautes passionnés par ce sport qui ont accumulé une quantité incroyable de données accessibles sur des sites tels www.basketballvalue.com ou www.shrpsports.com (rappelant l’engouement de certains pour les réseaux de métro). Ainsi, sur cette période, les basketteurs américains ont marqué en moyenne 94,78 paniers par match, soit environ 0,033 panier à chaque seconde de jeu (un match se composant de quatre périodes de 12 minutes). Mais les basketteurs ne sont pas réglés comme des coucous suisses, et cette moyenne cache une grande variabilité quand au rythme auquel les ballons rentrent dans l’anneau.
Il apparaît ainsi que la durée séparant deux paniers suit une loi exponentielle simple : un seul paramètre suffit à modéliser le rythme des matchs, ce qui va sans doute décevoir les spectateurs qui attendent fébrilement le prochain panier de leur équipe. Cette loi de probabilité, appelée loi de Poisson, est bien connue du monde de la physique, car elle sert notamment à décrire la fréquence de désintégration d’un noyau radioactif. Cette loi explique en termes mathématiques qu’il est plus probable de voir une contre-offensive rapide qu’une phase de jeu particulièrement calme, même si les annales de la NBA gardent trace d’un intervalle vierge de 402 secondes, soit plus de la moitié d’une période sans panier marqué ! Mais cette loi signifie aussi que le fait de marquer à un instant t est très faiblement corrélé à ce qui a précédé au cours de la période : le score semble résulter d’un processus aléatoire homogène, et les éventuelles accélérations dans le jeu ne sont ainsi que le reflet des fluctuations de cette loi statistique et non des revirements stratégiques.
Peut-on prédire le résultat d’un match ?
Au-delà des considérations sur le rythme du match, peut-on construire des modèles sur l’évolution du score entre les deux équipes ? Pour les deux chercheurs américains, celui-ci est déterminé par trois facteurs qui viennent enrichir ce processus aléatoire. Il apparaît tout d’abord qu’il est plus probable qu’une contre-offensive suive un panier que la même équipe marque deux fois de suite, une séquence qui ne se réalise que dans 34,8 % des cas. Un tel scénario est appelé en physique statistique une marche aléatoire anti-persistante : le marcheur, qui avance aléatoirement d’un côté ou de l’autre d’une ligne, préfère changer de direction à chaque pas plutôt que de poursuivre sa route dans le même sens.
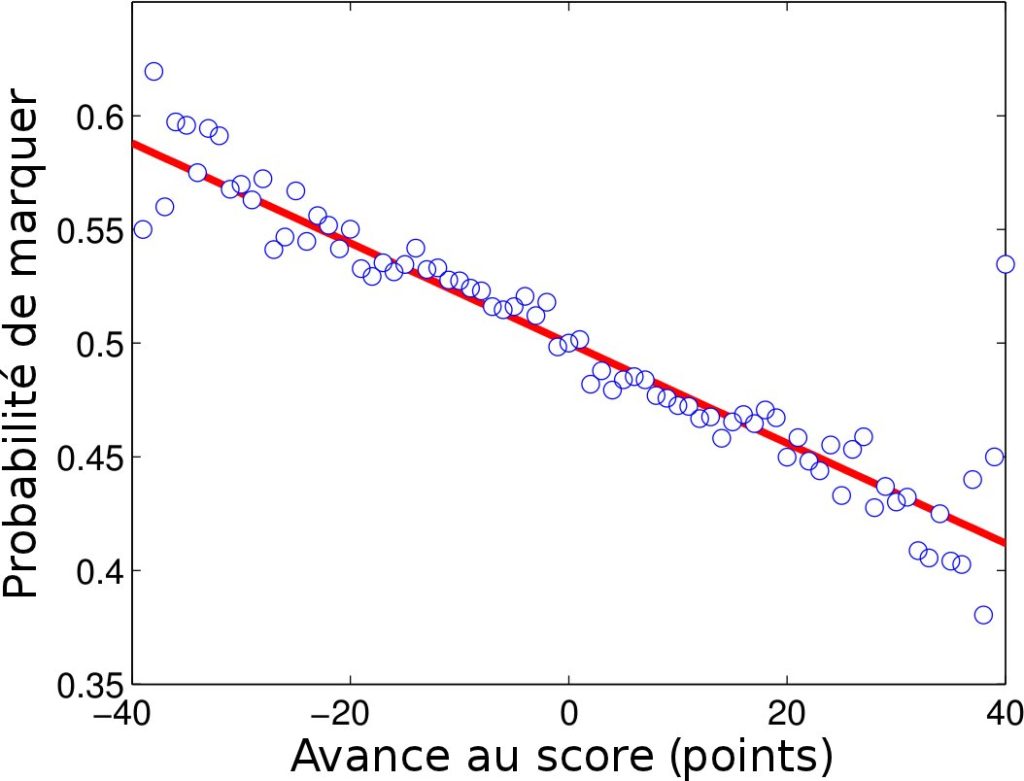
Le second facteur mis en avant est l’existence d’une “force de rappel” (comme la force élastique d’un ressort) qui entraîne une équipe menée au score à marquer un panier avec une probabilité plus grande que l’équipe en tête. Cet “avantage” est d’autant plus grand que l’équipe est largement distancée au panneau d’affichage. Un résultat qui se comprend aisément : une équipe menée va chercher à marquer pour rattraper son retard, quand l’équipe qui mène jouera la montre afin de conserver son avance. Cette logique sportive coïncide avec une loi statistique connue des physiciens sous le nom de processus d’Ornstein-Uhlenbeck, utilisé également en ingénierie financière pour anticiper l’évolution des taux d’intérêts.
Enfin, un dernier facteur introduit une différence de niveau entre le deux équipes : dans deux matchs sur trois, l’équipe victorieuse est celle qui aura accompli la meilleure saison. En d’autres termes, la meilleure équipe a plus de chances de gagner… mais cette différence de niveau est en général trop faible pour prédire le résultat d’un match quelconque du championnat de NBA. Pour les deux chercheurs, “il est difficile de déterminer quelle équipe est supérieure en observant un match classique, et quasi impossible en ne regardant qu’une courte période de jeu”.
Ces trois facteurs fournissent néanmoins une base pour la simulation numérique d’une saison complète de la NBA, où le seul paramètre introduit arbitrairement par les chercheurs est le niveau intrinsèque de chaque équipe. Ce championnat numérique se rapproche de façon étonnante de la vraie compétition sportive. Dans les deux cas, une équipe mène souvent pendant la totalité du match, ce qui n’empêche pas un retournement de dernière minute : cette loi statistique découverte par Paul Lévy en 1939 est appelée loi de l’arcsinus, et s’applique également au dépouillement d’un scrutin (vous pouvez retrouver ici une vidéo expliquant ce processus en détail).
Alchimie subtile entre talent, chance et force physique pour les fans et les joueurs, le basket-ball se révèle ainsi sous le regard des physiciens un simple jeu de lois statistiques, mais tout aussi passionnant à regarder en traçant des distributions de probabilités et en résolvant des équations de marches aléatoires…
Source : Alan Gabel et Sidney Redner, Random Walk Picture of Basketball Scoring, arXiV, 12 janvier 2012.
Crédit photo : U.S. Navy photo, 2nd Class Damon J. Moritz.





