Il existe parfois un long chemin entre une preuve empirique, fondée sur des observations, et sa démonstration physique, résultat de calculs et de simulations. Un physicien français, Christophe Eloy, de l’Institut de Recherche sur les Phénomènes Hors Équilibre (IRPHE), vient ainsi d’apporter une explication à une règle édictée par Léonard de Vinci il y a cinq siècles. À partir de ses études botaniques sur les arbres, le savant italien avait déduit une relation mathématique entre la taille du tronc et celle des branches qui en partent. Selon lui, la section du tronc de l’arbre est égale à la somme des sections de toutes les branches prises à un étage donné de l’arborescence. En termes mathématiques, cette “règle de Léonard” se traduit par la formule suivante : D2 = ∑di2, où D est le diamètre du tronc qui se subdivise en n branches de diamètre noté di (l’indice i prenant les valeurs 1, 2, … n pour chacune des branches). Deux questions se posent alors : cette relation est-elle correcte ? et d’où provient-elle ?
De nombreux physiciens se sont attelés à la résolution de ce problème, parmi lesquels Benoît Mandelbrot, le père des objets fractals, et ont montré que la règle de Léonard se vérifiait pour un grand nombre d’espèces, avec un exposant (égal à 2 dans la règle originale) pouvant varier entre 1,8 et 2,3. Suite à ces travaux, plusieurs explications ont été proposées, se fondant soit sur des raisonnements hydrauliques (la sève doit monter jusqu’en haut de l’arbre) ou sur des considérations mécaniques relatives à la flexion des branches sous leur propre poids. Christophe Eloy suggère une autre origine : la thigmomorphogenèse. Sous ce vocable barbare se cache le fait que la croissance d’une plante peut être gouvernée par des contraintes d’ordre mécanique, parmi lesquelles le vent qui souffle sur ses branches.
“Je plie, et ne romps pas.”
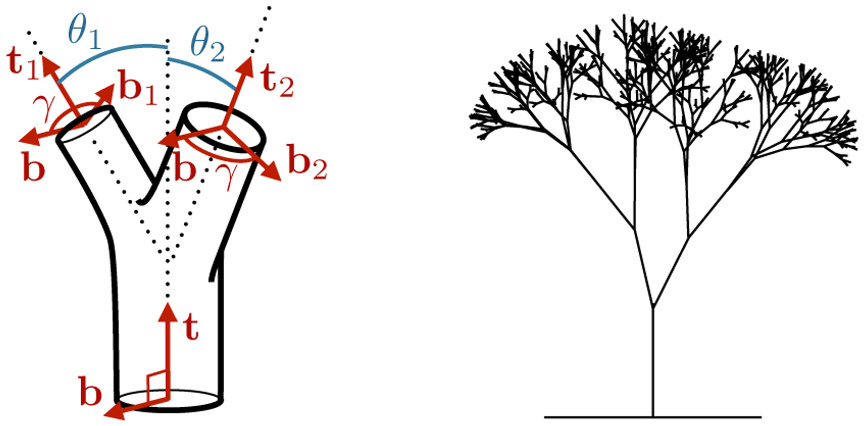
Ainsi, la force qui guiderait l’architecture d’un arbre et les dimensions de ses branches serait la pression exercée par le vent sur celles-ci : les branches doivent éviter la rupture face aux bourrasques pour sauvegarder l’intégrité de l’arbre. Des considérations analogues à celles faites par les ingénieurs en travaux publics pour veiller à la solidité d’édifices comme la Tour Eiffel. Pour en revenir au domaine végétal, la géométrie de l’arbre est décrite par un modèle mathématique rassemblant deux ingrédients : la règle de Léonard, donnant le diamètre des branches, et la nature fractale supposée de l’arbre, établissant leurs longueurs. La structure ainsi modélisée sert de base aux calculs du physicien français, fondés sur l’hypothèse que l’arbre doit résister à la pression du vent, et que cette résistance à la rupture est partout équivalente, du tronc aux feuilles les plus périphériques. La probabilité de rupture, modélisée par une loi statistique dite de Weibull, est donc maintenue constante à chaque étage, ce qui permet de déterminer l’exposant de la règle de Léonard : il se situe d’après les calculs autour de 2, la valeur prédite par de Vinci ! L’hypothèse thigmomorphogénétique semble donc expliquer la règle multiséculaire établie par de Vinci.
Un modèle numérique en trois dimensions, introduisant une certaine variabilité dans l’orientation et la longueur des branches issues du tronc, confirme là aussi la règle de Léonard. En supposant que la résistance au vent (ou de façon moins optimiste, la probabilité de rupture) est égale pour tous les étages de l’arbre, la simulation calcule la section de chaque branche et détermine l’exposant de Léonard, là aussi voisin de 2. Cette structure fractale garantit donc les meilleures chances de résister à la pression éolienne pour que les arbres “plient, et ne rompent pas”.
Source : C. Eloy, Leonardo’s rule, self-similarity, and wind-induced stresses in trees, Physical Review Letters, 7 novembre 2011.





